Πόση ευτυχία αγοράζουν τα χρήματα;

Φανταστείτε ένα παιχνίδι στο οποίο ρίχνετε το ζάρι και κερδίζετε τον αριθμό των δολαρίων της ζαριά σας. Έτσι, αν φέρετε ένα, κερδίζετε 1 δολάριο, αν φέρετε δύο, κερδίζετε 2 δολάρια κ.ο.κ. Πόσο πρέπει να πληρώσετε για να παίξετε;

Όσοι πρόσεχαν στο μάθημα των πιθανοτήτων γνωρίζουν ήδη την απάντηση. Τα πιθανά αποτελέσματα είναι 1, 2, 3, 4, 5 ή 6 δολάρια, καθένα από τα οποία έχει μία στις έξι πιθανότητες να προκύψει. Τα αναμενόμενα κέρδη σας είναι το άθροισμα κάθε αποτελέσματος πολλαπλασιασμένο με τις πιθανότητες εμφάνισής του. Αν τα προσθέσετε όλα μαζί, το ποσό ανέρχεται σε 3,50 δολάρια. Έτσι έχετε την τιμή σας: αν μπορείτε να παίξετε πληρώνοντας λιγότερο από 3,50 δολάρια, αξίζει. Για παράδειγμα, αν μπορείτε να πληρώσετε 3 δολάρια για να παίξετε, τότε κατά μέσο όρο θα έχετε καθαρό κέρδος 0,50 δολάρια.

Ωραίο, αλλά όχι αρκετό ώστε η αγωνία σας να χτυπήσει κόκκινο. Εξάλλου, υπάρχει 50% πιθανότητα να μην βγάλετε τίποτα ή ακόμα και να χάσετε. Άλλωστε, με λίγα δολάρια δεν μπορείς να κάνεις και πολλά. Όμως, ας υποθέσουμε ότι σας προσφέρονται 10.000 ζαριές. Πολύ πιο ενδιαφέρον, δεν νομίζετε;. Η διαίσθησή σας λέει ότι τώρα είναι βέβαιο ότι θα έχετε μέσο όρο κοντά στα 3,50 δολάρια ανά ζαριά, αφού η επανάληψη θα εξομαλύνει τις «ατυχίες». Ένας μαθηματικός θα επιβεβαίωνε το ένστικτό σας: με τόσες πολλές ζαριές, οι πιθανότητες ο μέσος όρος να πέσει πολύ μακριά από τα 3,50 δολάρια είναι σχεδόν μηδενικές. Με άλλα λόγια, αν κάθε ζαριά κοστίζει 3 δολάρια, έχετε σχεδόν εγγυημένο κέρδος περίπου 5.000 δολάρια (ή 10.000 παρτίδες των 0,50 δολαρίων). Θα ήσασταν ανόητος αν απορρίπτατε μια τέτοια συμφωνία – τόσο πολύ που, αν δεν είχατε τα 30.000 δολάρια που απαιτούνται για να παίξετε, θα έπρεπε να τα δανειστείτε.

Σκεφτείτε τώρα μια τελευταία παραλλαγή: αντί για 10.000 ζαριές, επιστρέφετε σε μία μόνο. Αυτή τη φορά, όμως, τα κέρδη σας θα είναι 10.000 δολάρια επί το σκορ των ζαριών και το κόστος του παιχνιδιού είναι 30.000 δολάρια. Πόσο τυχερός αισθάνεσθε τώρα; Το αναμενόμενο κέρδος εξακολουθεί να είναι 5.000 δολάρια, αλλά ο κίνδυνος να χάσετε τουλάχιστον 10.000 δολάρια (φέρνοντας άσσο ή δύο) έχει αυξηθεί από σχεδόν μηδέν σε ένα προς τρία. Παρά το προσδοκώμενο κέρδος, οι περισσότεροι μάλλον θα αποχωρούσαν.

Αυτό που ενώνει και τα τρία παιχνίδια είναι ο λόγος του αναμενόμενου κέρδους προς την αρχική δαπάνη. Σε κάθε περίπτωση είναι 17%, ή 0,50 δολάρια διαιρούμενο με 3 δολάρια. Γιατί, λοιπόν, προκαλούν τόσο διαφορετικές αντιδράσεις; Η απάντηση είναι ότι εμπεριέχουν διαφορετικά ποσοστά κινδύνου. Το στοίχημα των 30.000 δολαρίων σε μία μόνο ζαριά είναι σαφώς πιο επικίνδυνο από το στοίχημα των 3 δολαρίων. Ωστόσο κατανέμοντας τα 30.000 δολάρια σε 10.000 ζαριές, καθιστώντας τις πιθανότητες απώλειας αμελητέες, το στοίχημα δεν έχει νόημα. Τόσο για τους παίκτες όσο και για τους επενδυτές, το μάθημα είναι ξεκάθαρο. Δεν είναι μόνο οι αναμενόμενες αποδόσεις που έχουν σημασία, αλλά και το ρίσκο που πρέπει να αναλάβετε για να τις αποκτήσετε.

Τέτοια επινοημένα παιχνίδια μπορεί να φαίνονται ανόητα. Στην πραγματικότητα, οπλισμένοι με κάτι περισσότερο από τις αρχές που κρύβονται πίσω από αυτά και κάποια μαθηματικά που έχουν λυθεί εδώ και μισό αιώνα, μπορείτε να δημιουργήσετε μια ολόκληρη θεωρία για το πώς να επενδύσετε τις αποταμιεύσεις που αποκτήσατε με κόπο. Σας λένε πόσα πρέπει να ρισκάρετε στο χρηματιστήριο, πόσα να κρατήσετε σε ασφαλές μέρος και τι μπορείτε να ξοδέψετε στη σύνταξη. Απαιτούνται μόνο μερικά στοιχεία που αφορούν τις χρηματοπιστωτικές αγορές και μερικά από τα πιο απλά και φτηνά επενδυτικά κεφάλαια που προσφέρουν οι διαχειριστές περιουσιακών στοιχείων. Επιπλέον, αυτή η προσέγγιση διατυπώθηκε για πρώτη φορά από έναν νομπελίστα οικονομολόγο και σήμερα είναι σχεδόν καθολικά αποδεκτή από τους διαδόχους του ως η «σωστή» προσέγγιση για τις επενδύσεις και τις δαπάνες. Ωστόσο, εκτός του ακαδημαϊκού χώρου, σχεδόν κανείς δεν την έχει ακούσει.

Η τάση που εξηγεί γιατί κάθε παιχνίδι με ζάρια προκαλεί διαφορετική αντίδραση είναι γνωστή ως «φθίνουσα οριακή χρησιμότητα του πλούτου». Είναι ένας πομπώδης τρόπος να πούμε ότι όσο περισσότερα χρήματα έχουμε ήδη, τόσο λιγότερο μας αρέσει να αποκτούμε ακόμα περισσότερα. Για κάποιον που τα βγάζει πέρα δύσκολα, 1 εκατομμύριο δολάρια θα του αλλάξουν τη ζωή, αλλά ένα δεύτερο εκατομμύριο βελτιώνει το βιοτικό του επίπεδο πολύ λιγότερο, κι ένα τρίτο κάνει κάποιον απλώς λίγο πλουσιότερο.

Για να δείτε τη σύνδεση με τον τζόγο, σκεφτείτε πόσο πρόθυμος μπορεί να είναι ένας πρόσφατα εκατομμυριούχος να τα ποντάρει όλα σε μία ζαριά. Η νίκη μπορεί να σημαίνει ένα μεγαλύτερο σπίτι – αλλά η χαρά των ήδη αποκτηθέντων είναι μεγαλύτερη από τον πόνο της ήττας, που θα σήμαινε την επιστροφή στην πείνα. Ακόμα και αν το διακύβευμα μειώνονταν στο μισό, οι περισσότεροι θα απέφευγαν το παιγνίδι. Αυτό προκύπτει από τη φθίνουσα οριακή χρησιμότητα του πλούτου. Ένα ρίσκο 50/50 σε ένα μεγάλο κομμάτι των αποταμιεύσεών σας, ακόμα και αν μπορεί να κερδίσετε το ίδιο ποσό, δεν αξίζει τον κόπο. Τα ποσά σε δολάρια είναι ίσα, αλλά ο αντίκτυπος της απώλειας θα ήταν μεγαλύτερος.

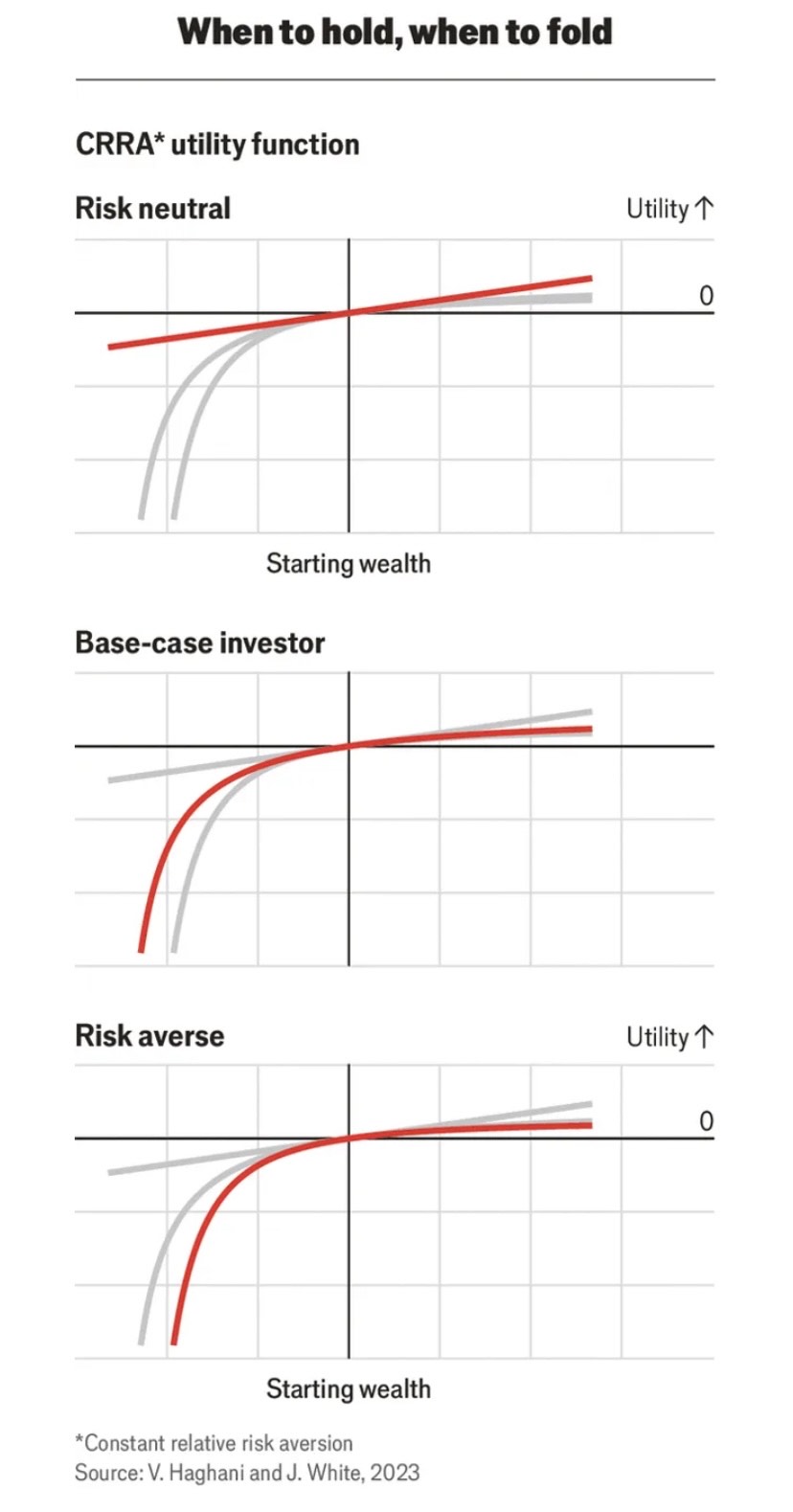
Η έκβαση είναι λιγότερο προφανής: δηλαδή, ο ρυθμός με τον οποίο μειώνεται η απόλαυση του νέου πλούτου καθώς γίνεστε πλουσιότεροι και η αποστροφή σας για το ρίσκο μεγάλων ποσών είναι οι δύο όψεις του ίδιου νομίσματος. Οι δύο αυτές όψεις μπορούν να αποτυπωθούν με μία μόνο παράμετρο σε μια οικογένεια «συναρτήσεων χρησιμότητας», οι οποίες περιγράφουν την ευχαρίστηση που αντλείται από διαφορετικά ποσά πλούτου. Οι ερευνητές έχουν διαπιστώσει ότι αυτές οι συναρτήσεις χρησιμότητας «σταθερής σχετικής αποστροφής στον κίνδυνο» (CRRA) ταιριάζουν αρκετά καλά στη στάση των περισσότερων ανθρώπων απέναντι στον πλούτο. Η παράμετρος, γνωστή ως «αποστροφή κινδύνου», μπορεί να βαθμονομηθεί ανάλογα με το επίπεδο τόλμης κάθε ατόμου. Το Διάγραμμα 1 παρουσιάζει τις συναρτήσεις χρησιμότητας CRRA για ένα εύρος αποστροφής κινδύνου.

Το παραπάνω εξηγεί γιατί το ρίσκο έχει σημασία στα παιχνίδια με ζάρια. Όμως, τι σχέση έχουν όλα αυτά με τις επενδύσεις; Αυτό το ανέλυσε ο Robert Merton, ο οποίος αργότερα κέρδισε το βραβείο Νόμπελ Οικονομικών, σε μια εργασία του το 1969. Ο εύστοχος τίτλος του «Lifetime Portfolio Selection Under Uncertainty: The Continuous-Time Case» έδειξε πώς μια συνάρτηση χρησιμότητας CRRA, βαθμονομημένη με βάση την αποστροφή κάθε ατόμου προς τον κίνδυνο, θα μπορούσε να μεταφραστεί σε ένα χαρτοφυλάκιο με βέλτιστη κατανομή μεταξύ περιουσιακών στοιχείων υψηλής απόδοσης αλλά υψηλού κινδύνου, όπως οι μετοχές, και ασφαλών περιουσιακών στοιχείων, όπως τα ομόλογα. Στη διαδικασία του κ. Merton, «βέλτιστο» σημαίνει εξισορρόπηση της επιθυμίας του ατόμου για αποδόσεις και της αποστροφής του στον κίνδυνο κατά τρόπο ώστε η αναμενόμενη ευτυχία του να μεγιστοποιείται.

Η μεγιστοποίηση της ευτυχίας ακούγεται ωραίο. Η διαδικασία του κ. Merton έχει μερικά ακόμα πιο ωραία χαρακτηριστικά. Οι πιο συνηθισμένες συμβουλές προς τους μικροεπενδυτές για τον διαχωρισμό των αποταμιεύσεων μεταξύ μετοχών και ομολόγων μπορεί να φαίνονται αυθαίρετες. Πρόκειται για τον κανόνα «60/40», ο οποίος υποστηρίζει 60% μετοχές και 40% ομόλογα – αλλά γιατί 60/40 και όχι 70/30 ή 50/50; Οι πιο διαισθητικοί κανόνες λένε όσοι αποταμιεύουν για συνταξιοδότηση να μειώνουν σταδιακά την έκθεσή τους στο χρηματιστήριο όσο μεγαλώνουν, καθώς έτσι έχουν λιγότερο χρόνο να συμπληρώσουν τις αποταμιεύσεις τους σε περίπτωση κραχ. Θα μπορούσατε, ας πούμε, να διατηρείτε ένα ποσοστό του χαρτοφυλακίου σας ίσο με την ηλικία σας σε ομόλογα και το υπόλοιπο σε μετοχές. Αλλά γιατί θα πρέπει να είναι η ηλικία σας και όχι, ας πούμε, η ηλικία σας συν ή μείον πέντε;

Το «μερίδιο Merton» υπολογίζει το ποσοστό ενός χαρτοφυλακίου που πρέπει να τοποθετηθεί σε επικίνδυνα περιουσιακά στοιχεία από παράγοντες που είναι προφανώς σχετικοί. Λέει ότι το μερίδιο σε επικίνδυνα περιουσιακά στοιχεία πρέπει να ισούται με την υπερβάλλουσα αναμενόμενη απόδοση τους σε σχέση με εκείνη της ασφαλούς εναλλακτικής λύσης, διαιρούμενη τόσο με την αποστροφή του επενδυτή προς τον κίνδυνο όσο και με το τετράγωνο της μεταβλητότητας των επικίνδυνων περιουσιακών στοιχείων. Ο κ. Merton το έδειξε αρχικά για ένα χαρτοφυλάκιο δύο περιουσιακών στοιχείων (επικίνδυνο και ασφαλές). Ένα πραγματικό παράδειγμα θα ήταν ένα χαρτοφυλάκιο που αποτελείται από ένα παγκόσμιο αμοιβαίο κεφάλαιο παρακολούθησης μετοχών και ένα μακροπρόθεσμο αμοιβαίο κεφάλαιο κρατικών ομολόγων.

Αν ο ορισμός του μεριδίου Merton φαίνεται υπερβολικός, σκεφτείτε τι συνεπάγεται. Εάν η απόδοση του ασφαλούς περιουσιακού στοιχείου μειωθεί, ίσως επειδή τα επιτόκια πέφτουν, αλλά η αναμενόμενη απόδοση των μετοχών παραμένει η ίδια, θα πρέπει να επενδύσετε περισσότερα στο χρηματιστήριο. Είναι λογικό: το κόστος ευκαιρίας της διακράτησης ομολόγων έναντι των μετοχών μόλις αυξήθηκε. Αντίθετα, αν η μεταβλητότητα της χρηματιστηριακής αγοράς εκτοξεύεται, π.χ. επειδή μια τραπεζική κρίση βρίσκεται σε εξέλιξη, θα πρέπει να πουλήσετε μερικές μετοχές για να αγοράσετε ομόλογα. Όπως και με τη ζαριά των 30.000 δολαρίων, οι πιθανότητες μεγάλων κερδών ή ισοδύναμων ζημιών μόλις αυξήθηκαν – αλλά ο πόνος των ζημιών θα υπερτερούσε της ευχαρίστησης των κερδών.

Το μερίδιο Merton είναι ακόμα πιο διδακτικό για τα ευρύτερα διδάγματά του σχετικά με τις επενδύσεις. Εκτός από σπάνιες περιπτώσεις, όλοι όσοι έχουν αποταμιεύσεις θα πρέπει να αγοράζουν τουλάχιστον μερικές μετοχές. Εφόσον η αναμενόμενη απόδοσή τους είναι μεγαλύτερη από την απόδοση των ακίνδυνων ομολόγων, το μερίδιο Merton είναι πάντα μεγαλύτερο από το μηδέν. Η άλλη πλευρά είναι ότι, πολύ σπάνια, κανείς δεν πρέπει να έχει μετοχές. Τα τέλη της δεκαετίας του 1990, με της φούσκα των dotcom, είναι ένα παράδειγμα. Οι τιμές των μετοχών είχαν αυξηθεί τόσο αστρονομικά σε σχέση με τα υποκείμενα κέρδη που η αναμενόμενη απόδοση της αγοράς μετοχών ήταν χαμηλότερη από εκείνη των κρατικών ομολόγων, θέτοντας το μερίδιο Merton κάτω από το μηδέν. Οι επενδυτές που έλαβαν υπόψη τους και πούλησαν τις μετοχές τους πριν από την επακόλουθη κατάρρευση μάλλον θα φούσκωσαν από υπερηφάνεια για την επιλογή τους.

Ο John Campbell, καθηγητής οικονομικών στο Χάρβαρντ, επισημαίνει ότι το μερίδιο Merton συμβουλεύει επίσης κατά του «reaching for yield» (στόχευσης αποδόσεων μέσω υψηλότερου ρίσκου). Αυτή η ιδέα ήταν στη μόδα όταν τα επιτόκια ήταν κοντά στο μηδέν και περιελάμβανε τη συσσώρευση χαρτοφυλακίων γεμάτων επικίνδυνα περιουσιακά στοιχεία για να ενισχύσουν τις αποδόσεις. Ωστόσο, ένα άλλο μάθημα από τη μερίδιο Merton είναι ότι, κατά την απόφαση της κατανομής σας σε επικίνδυνα περιουσιακά στοιχεία, σημασία έχει το χάσμα μεταξύ των αναμενόμενων αποδόσεών τους και του επιτοκίου χωρίς κίνδυνο και όχι το απόλυτο επίπεδο. Οι χαμηλές αποδόσεις συνεπάγονται χαμηλά κέρδη, όχι ότι πρέπει ξαφνικά να γεμίσετε κίνδυνο.

Τέλος με τη θεωρία. Πώς, όμως, όλα αυτά λειτουργούν στην πράξη; Με βάση τις μακροχρόνιες ιστορικές αποδόσεις, πράγματι πολύ καλά. Ο Victor Haghani και ο James White, συν-συγγραφείς του βιβλίου «The Missing Billionaires», το οποίο προσπαθεί να εκλαϊκεύσει τις ιδέες του κ. Merton, έχουν επεξεργαστεί τους αριθμούς. Πήραν έναν δείκτη αμερικανικών μετοχών ως το επικίνδυνο περιουσιακό στοιχείο και τα προστατευμένα από τον πληθωρισμό κρατικά ομόλογα ως το ασφαλές, χρησιμοποιώντας δεδομένα από το 1900 έως το 2022 (χρησιμοποιώντας ένα υποκατάστατο για τα ομόλογα πριν από το 1997, όταν εκδόθηκαν για πρώτη φορά). Στη συνέχεια συνέκριναν το χαρτοφυλάκιο μεριδίου Merton με ένα χαρτοφυλάκιο που μοιράζεται κατά 65/35 μεταξύ μετοχών και ομολόγων.

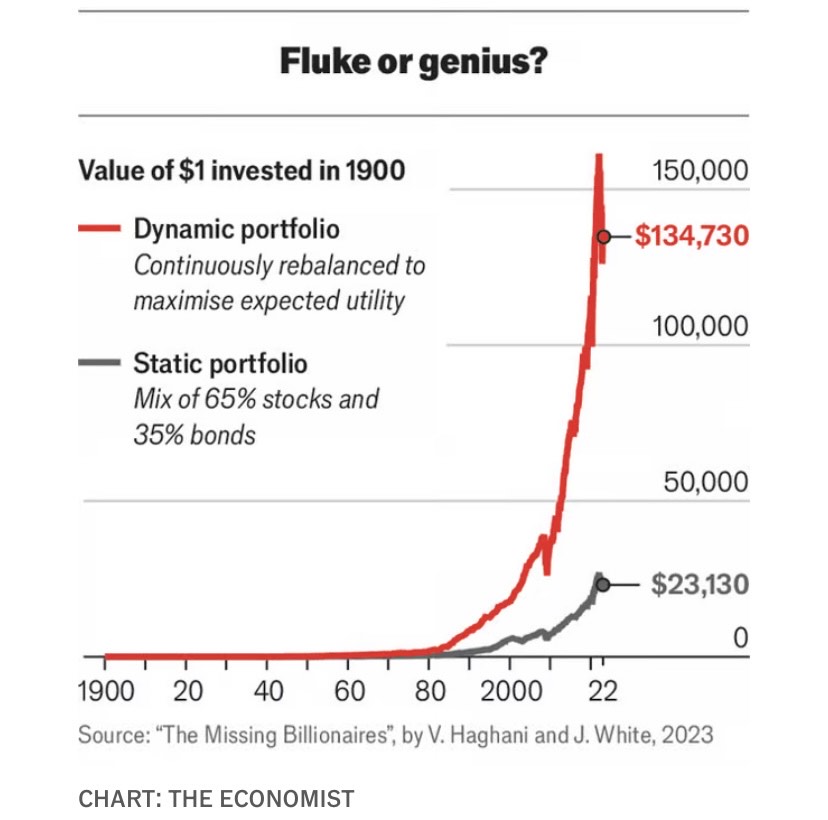
Τα αποτελέσματα παρουσιάζονται στο διάγραμμα 2. Το χαρτοφυλάκιο Merton θα κέρδιζε το χαρτοφυλάκιο 65/35, επιτυγχάνοντας ετήσια απόδοση 10% έναντι 8,5%. Ακόμα πιο αξιοσημείωτο είναι ότι θα είχε μεγαλύτερη απόδοση από τη στρατηγική του 100% σε μετοχές, πέραν του ότι συνεπάγεται 40% μικρότερο κίνδυνο. Οι παρελθούσες αποδόσεις, φυσικά, δεν αποτελούν τέλειο οδηγό για τις μελλοντικές, και ίσως η στρατηγική Merton να ήταν απλώς τυχερή. Όμως με τη θεωρία και την ιστορία να δείχνουν προς την ίδια κατεύθυνση, αυτό φαίνεται μάλλον απίθανο.

Πιθανώς το πιο ελκυστικό χαρακτηριστικό του μεριδίου Merton είναι η συνταγή του για την ανταπόκριση στις μεταβαλλόμενες συνθήκες της αγοράς. Μια επενδυτική στρατηγική που προσαρμόζεται υπό το πρίσμα νέων πληροφοριών – όπως μια πτώση των τιμών που αυξάνει τις αναμενόμενες αποδόσεις- είναι μια στρατηγική που πολλοί θα βρουν ευκολότερο να τηρήσουν. Κάτι τέτοιο συμβάλλει στην αποφυγή της παγίδας της συνεχούς αλλαγής στρατηγικής, η οποία καθιστά τους επενδυτές ευάλωτους σε ένστικτα που καταστρέφουν τον πλούτο, όπως η παρόρμηση να πουλήσουν τα πάντα κατά τη διάρκεια ενός κραχ. Αντίθετα, μπορούν να ακολουθήσουν μια καθορισμένη διαδικασία και να αποφύγουν τέτοιες παγίδες.

Όλα αυτά δημιουργούν έναν γρίφο. Σχεδόν όλοι όσοι σπουδάζουν μεταπτυχιακά χρηματοοικονομικά, λέει ο John Cochrane του Πανεπιστημίου του Στάνφορντ, θα μάθουν για το πλαίσιο του κ. Merton. Ωστόσο, μεταξύ των επαγγελματιών, και ιδίως των διαχειριστών περιουσίας, είναι αξιοσημείωτα ανεπαρκώς υιοθετημένο και συχνά άγνωστο. Ο κ. Haghani ενσαρκώνει αυτό το χάσμα, αφού συνεργάστηκε με τον κ. Merton τη δεκαετία του 1980 πριν ιδρύσει μαζί του ένα hedge fund, το Long-Term Capital Management (LTCM). Παρά ταύτα, λέει ο κ. Haghani, μόνο όταν το LTCM τινάχτηκε στον αέρα με θεαματικό τρόπο – εξαφανίζοντας ένα προσωπικό μέρισμα, που το μερίδιο Merton θα του έλεγε ότι ήταν πολύ μεγάλο – κατάλαβε αυτή την πτυχή της εργασίας του πρώην συναδέλφου του.

Ένας λόγος γι’ αυτό, υποστηρίζει ο κ. Cochrane, είναι ότι οι απαιτούμενοι υπολογισμοί είναι εξαιρετικά ευαίσθητοι ως προς τις εισροές, οι οποίες με τη σειρά τους είναι δύσκολο να εκτιμηθούν. Ένα παράδειγμα είναι η μεταβλητότητα στο μερίδιο Merton. Αυτή δεν είναι άμεσα παρατηρήσιμη από την αγορά και, δεδομένου ότι ο υπολογισμός περιλαμβάνει το τετράγωνό της, ένα μικρό σφάλμα αλλάζει πολύ την προβλεπόμενη κατανομή. Παρομοίως, η εκτίμηση των αναμενόμενων αποδόσεων των μετοχών ή των συσχετίσεων μεταξύ επικίνδυνων περιουσιακών στοιχείων μπορεί να είναι εφιαλτική.

Παρόλα αυτά, μπορούν να υπάρξουν και παραποιήσεις. Το ριψοκίνδυνο περιουσιακό σας στοιχείο μπορεί απλώς να είναι ένα αμοιβαίο κεφάλαιο που παρακολουθεί έναν ευρύ δείκτη τιμών μετοχών. Η μεταβλητότητα μπορεί να εκτιμηθεί ως συστατικό του μακροχρόνιου ιστορικού επιπέδου της (περίπου 20% για το αμερικανικό χρηματιστήριο) και του βραχυπρόθεσμου δείκτη VIX, ο οποίος μετράει πόσο πληρώνουν οι traders για να ασφαλιστούν έναντι μεγάλων διακυμάνσεων των τιμών. Μια ατελής, αλλά λογική, πρόβλεψη των αναμενόμενων αποδόσεων των μετοχών είναι το αντίστροφο του κυκλικά προσαρμοσμένου λόγου τιμής-κερδών που διαδόθηκε από τον Robert Shiller του Πανεπιστημίου Yale. Εάν το «ασφαλές» περιουσιακό σας στοιχείο είναι τα κρατικά ομόλογα, το αναμενόμενη κέρδος είναι απλώς η απόδοση.

Ένα μεγαλύτερο πρόβλημα είναι ότι η συνταγή του μεριδίου Merton είναι μερικές φορές τρελή για τους μικροεπενδυτές. Ο καθηγητής Campbell του Χάρβαρντ σημειώνει ότι ενίοτε προτείνει μια ανοιχτή θέση (short position), την οποία οι ιδιώτες συχνά δεν μπορούν να υιοθετήσουν και η οποία μπορεί να οδηγήσει σε απεριόριστες απώλειες. Αν πρόκειται να υπολογιστεί αυστηρά, απαιτεί επίσης μια εκτίμηση του ανθρώπινου κεφαλαίου του ατόμου, ή του αθροίσματος των αναμενόμενων μελλοντικών αποδοχών του. Για τους νέους, αυτό μπορεί να είναι η συντριπτική πλειονότητα του συνολικού τους κεφαλαίου, και λογικά «ασφαλές». Κατά συνέπεια, η τήρηση της κατανομής του μεριδίου Merton για τα επικίνδυνα περιουσιακά στοιχεία μπορεί να απαιτήσει από αυτούς να δανειστούν για να αγοράσουν μετοχές. Και πάλι, πολλοί δεν είναι σε θέση να το κάνουν, και ακόμα και να μπορούν, θα διακινδύνευαν να χρεοκοπήσουν αν οι τιμές μεταβάλλονταν απότομα. Η αποφυγή τέτοιων κινδύνων σημαίνει την επιβολή ορίων, όπως ο καθορισμός του μεριδίου στο 0% ή στο 100%, εάν ποτέ πέσει εκτός αυτού του εύρους.

Ο κ. White, ο οποίος μαζί με τον κ. Haghani διευθύνει μια εταιρεία διαχείρισης πλούτου που εφαρμόζει τις ιδέες του κ. Merton στην πράξη, προσφέρει μια εύλογη εξήγηση για την ανεπαρκή υιοθέτησή τους: δεν είναι προς το συμφέρον των διαχειριστών. Για να κατανοήσει κανείς αυτό το πλαίσιο και να το υιοθετήσει μακροπρόθεσμα χρειάζεται χρηματοοικονομική εξειδίκευση. Ελάχιστοι διαχειριστές χρημάτων επιθυμούν να περιορίσουν με αυτόν τον τρόπο τη δεξαμενή των δυνητικών πελατών τους. Επιπλέον, η μεγιστοποίηση των αναμενόμενων αποδόσεων προσαρμοσμένων στον κίνδυνο μπορεί να είναι δύσκολη υπόθεση, όταν πολλοί πελάτες θέλουν απλώς το χρηματιστήριο να τους κάνει πλούσιους. Οι νέοι επενδυτές προτιμούν ιδιαίτερα τη νοοτροπία «δισεκατομμυριούχος ή ταπί», λέει ο κ. White. Για αυτούς, οι σταδιακές βελτιώσεις του πλαισίου Merton είναι λιγότερο σέξι από το να προσπαθούν να διαλέξουν την επόμενη Apple.

Κι εδώ βλέπουμε το παράδοξο των ιδεών του κ. Merton. Αν και υποτίθεται ότι βασίζονται στη στάση των επενδυτών απέναντι στον κίνδυνο και τον πλούτο, δεν ταιριάζουν με αυτό που πολλοί πραγματικοί επενδυτές λένε ότι θέλουν. Ένα άλλο παράδειγμα είναι ένας κανόνας δαπανών που υπονοείται από το πλαίσιο, ο οποίος λέει ότι κατά τη συνταξιοδότηση οι αποταμιευτές θα πρέπει να ξοδεύουν ένα καθορισμένο ποσοστό του πλούτου τους κάθε χρόνο και όχι ένα σταθερό ποσό σε δολάρια. Κάτι τέτοιο μειώνει τον κίνδυνο εξάντλησης του χαρτοφυλακίου σας πολύ γρήγορα, αλλά σημαίνει επίσης ότι οι δαπάνες σας πρέπει να κυμαίνονται ανάλογα με τις τιμές των περιουσιακών σας στοιχείων. Ελάχιστοι ενθουσιάζονται με αυτή την προοπτική, ωστόσο εξακολουθούν να επενδύουν σε μετοχές, οι τιμές των οποίων μπορεί να παρουσιάζουν μεγάλες διακυμάνσεις.

Το πρόβλημα, με άλλα λόγια, είναι η απροθυμία των ανθρώπων να αποδεχτούν τους συμβιβασμούς του πλαισίου Merton. Όμως οι συμβιβασμοί αυτοί είναι αναπόφευκτοι και αυτό που λένε οι επενδυτές ότι θέλουν είναι συχνά ανέφικτο. Οι θερμοκέφαλοι που αναζητούν τον επόμενο σούπερ σταρ της τεχνολογίας θα διαλέξουν ως επί το πλείστον τον λάθος άνθρωπο, και το «δισεκατομμυριούχος ή ταπί» ακούγεται λιγότερο γοητευτικό όταν χρεoκοπήσεις. Το να αρνείστε να συνδέσετε τις δαπάνες με την απόδοση του χαρτοφυλακίου σας είναι απλώς άρνηση της πραγματικότητας. Η δύναμη των μισού αιώνα παλιών ιδεών του κ. Merton είναι ότι αναγκάζουν τους επενδυτές να αντιμετωπίσουν αυτά τα γεγονότα κατά μέτωπο, ενώ παράλληλα επιδιώκουν τις καλύτερες αποδόσεις που μπορούν ρεαλιστικά να ελπίζουν. Παρά την αντιδημοτικότητά τους, σίγουρα αξίζουν μια δεύτερη ζαριά.

© 2024 The Economist Newspaper Limited. All rights reserved. Άρθρο από τον Economist, το οποίο μεταφράστηκε και δημοσιεύθηκε με επίσημη άδεια από την www.powergame.gr. Το πρωτότυπο άρθρο, στα αγγλικά, βρίσκεται στο www.economist.com

Διαβάστε επίσης

Ένας στους δύο νέους στην Ελλάδα θέλει να γίνει startupper

Επαγγέλματα: Το χάσμα στους μισθούς ανδρών και γυναικών

EY: Δέκα προκλήσεις και ευκαιρίες για τις εταιρείες εξόρυξης και μετάλλων το 2025

Ακολουθήστε το Powergame.gr στο Google News για άμεση και έγκυρη οικονομική ενημέρωση!