THEPOWERGAME


Μιλώντας για την ομορφιά των Μαθηματικών, δύσκολα κανείς μπορεί να προσδιορίσει σε τι ακριβώς αναφερόμαστε. Στον ενθουσιασμό στο τέλος μιας απόδειξης ή στον συσχετισμό φαινομενικά ετερόκλητων στοιχειών από τον κόσμο των μαθηματικών; Σε κάθε περίπτωση το έργο του Λέοναρτ Όιλερ συνδύασε και τις δύο εκδοχές και για αυτό δικαίως θεωρείται ένας από τους σημαντικότερους μαθηματικούς όλων των εποχών. Η συμβολή του Ελβετού μαθηματικού σε αρκετούς τομείς της μαθηματικής επιστήμης, όπως την ανάλυση, τη θεωρία αριθμών, την ευκλείδεια γεωμετρία, αλλά και τη θεωρία γραφημάτων, στην οποία υπήρξε προπάτορας, ήταν καθοριστική. Γι’ αυτό και διατρέχοντας το έργο του Όιλερ, θα συναντήσει κανείς ορισμένες αποδείξεις αλλά και ανακαλύψεις που υπήρξαν σταθμοί και σαγηνεύουν έως και σήμερα τη μαθηματική κοινότητα.
Μαθηματική ιδιοφυία από τα παιδικά του χρόνια
Ο Λέοναρντ Όιλερ γεννήθηκε στις 15 Απριλίου του 1707 στη Βασιλεία της Ελβετίας. Τα πρώτα ερεθίσματά του στα μαθηματικά τα έλαβε σε μικρή ηλικία από τον πατέρα του, Paul Euler, ο οποίος είχε φιλικές σχέσεις με την οικογένεια Bernouli. Σε ηλικία 13 ετών εγγράφεται στο πανεπιστήμιο της Βασιλείας, όπου, έχοντας ταυτόχρονα ως δάσκαλο τον Johan Bernouli, ολοκληρώνει τη διατριβή του σχετικά με τη σύγκριση των φιλοσοφιών του Καρτέσιου και του Νεύτωνα. Το 1726, σε ηλικία μόλις 19 ετών, συμμετέχει σε έναν διαγωνισμό της Γαλλικής Ακαδημίας Επιστημών σχετικά με την καλύτερη τοποθέτηση ιστίων σε ένα πλοίο, στον οποίο κερδίζει τη δεύτερη θέση, παρά την ισχνή επαφή του με τη ναυπηγική, χάνοντας από τον Πιέρ Μπουγκέ, Γάλλο φυσικό και μαθηματικό. Το 1727 μετακομίζει στην Αγία Πετρούπολη, ενώ το 1733 διαδέχεται τον Nicolaus Bernouli στην έδρα της Φυσιολογίας. Εξαιτίας των αναταραχών στη Ρωσία, μετακομίζει το 1741 στο Βερολίνο, δουλεύοντας για 25 χρόνια στην τοπική ακαδημία, στη διάρκεια των οποίων εκδίδει τα πιο σημαντικά του έργα: Την Εισαγωγή στην Απειροστική Ανάλυση (Introductio in analysin infinitorum, 1748) και τις Αρχές του Διαφορικού Λογισμού (Institutiones calculi differentialis, 1755).
Ο Λέοναρτ Όιλερ απεβίωσε στις 18 Σεπτεμβρίου του 1783 έπειτα από εγκεφαλικό επεισόδιο, έχοντας ήδη επιβαρημένη την υγεία του. Το τεράστιο όμως έργο των 75 τόμων, 45.000 σελίδων και 4.000 χειρογράφων αποτέλεσε παρακαταθήκη για τους μετέπειτα μαθηματικούς.
Ο τύπος του Όιλερ και η περίφημη ταυτότητά του (Euler’s Formula and Identity)
Ακολουθώντας τα βήματα του Βρετανού Roger Cotes, φυσικού και μαθηματικού, ο Όιλερ κατέληξε στο έργο του «Εισαγωγή στην Απειροστική Ανάλυση» με μια διαφορετική απόδειξη, χρησιμοποιώντας εκθετικές συναρτήσεις, στον περίφημο τύπο:
𝒊𝒙 = 𝒍𝒏(𝒄𝒐𝒔(𝒙) + 𝒊𝒔𝒊𝒏(𝒙)) (Roger)
ή
𝒆𝒊𝒙 = 𝐜𝐨𝐬 𝒙 + 𝒊𝒔𝒊𝒏(𝒙) (Euler)
Παρατηρούμε ότι με αυτούς τους τύπους συνδέονται οι λογαριθμικές (αντίστοιχα οι εκθετικές) συναρτήσεις με τριγωνομετρικές και φανταστικούς αριθμούς. Το αξιοσημείωτο εδώ είναι ότι ο Όιλερ, χρησιμοποιώντας τις γνωστές σειρές Taylor:
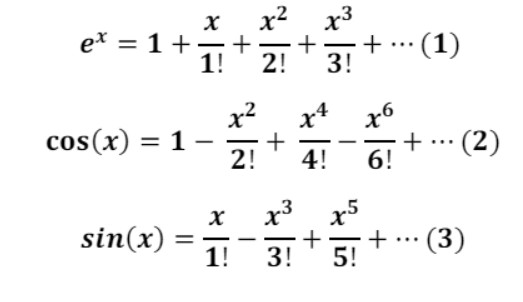
Για την εκθετική, συνημιτονοειδή και ημιτονοειδή αντίστοιχα συνάρτηση, παρατήρησε ότι αν προσθέσουμε κατά μέλη τις (2) και (3) προκύπτει περίπου η (1). Ο Όιλερ τότε συμπέρανε ότι αν πολλαπλασιάσουμε με τον κατάλληλο αριθμό κάποια από τις σειρές που αφορούν την ημιτονοειδή ή τη συνημιτονοειδή σειρά, θα προκύψει η σειρά της εκθετικής συνάρτησης. Έπειτα από παρατηρήσεις, κατέληξε στο ότι πρέπει να βρεθεί ένας αριθμός του οποίου το τετράγωνο ισούται με -1. Έτσι, δίνοντας τέλος στο δίλλημα για το αν πρέπει οι μιγαδικοί αριθμοί να γίνουν αποδεκτοί, η ιδέα των οποίων εισήχθη τον 16ο αιώνα από τον Gerolamo Gardano, ο Όιλερ ήταν ο πρώτος που χρησιμοποίησε το γνωστό σύμβολο ή για να αναπαραστήσει τη ρίζα του -1. Δηλαδή:
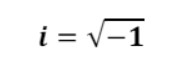
Και έτσι, πολλαπλασιάζοντας την ημιτονοειδή σειρά με το ί, κατέληξε στον γνωστό του τύπο.
Πώς όμως από τον τύπο αυτόν κατέληξε στην πιο μαγική ταυτότητα των μαθηματικών, την ![]()
Πολύ απλά, για x=π, ο τύπος γίνεται: 𝒆𝒊𝝅 = 𝐜𝐨𝐬 (𝝅) + 𝒊𝒔𝒊𝒏(𝝅)
Αλλά sin(π)=0 και cos(π)=-1, οπότε:
𝒆𝒊𝝅 = −𝟏
Ή 𝒆𝒊𝝅 + 𝟏 = 𝟎 𝒆𝒊𝝅 + 𝟏 = 𝒆𝒊𝝅 + 𝟏 = 𝟎
Αυτό το «κόσμημα», η «πιο αξιοσημείωτη ταυτότητα των μαθηματικών», όπως είπε ο Richard Feynman, αποτελεί μία από τις πιο γνωστές σχέσεις των μαθηματικών, η οποία συνδυάζει τα πιο σπουδαία σύμβολα, που φαινομενικά δεν συσχετίζονται κάπως μεταξύ τους, σε μία σχέση: τη σταθερά της εκθετικής συνάρτησης e, το σύμβολο της οποίας δόθηκε από το αρχικό γράμμα του επιθέτου του Όιλερ (Euler), τον αριθμό π που είναι ο λόγος της περιφέρειας ενός κύκλου προς τη διάμετρό του, τον φανταστικό αριθμό ί, το 1 που θεωρείται η αρχή των μετρήσεων και φυσικά το μηδέν, τον πιο θεμελιώδη αριθμό των μαθηματικών.
Το παράδοξο φυσικά είναι ότι ο Όιλερ δεν είχε διαπιστώσει τη μεγάλη γεωμετρική σημασία αυτής της αρχικής σχέσης:
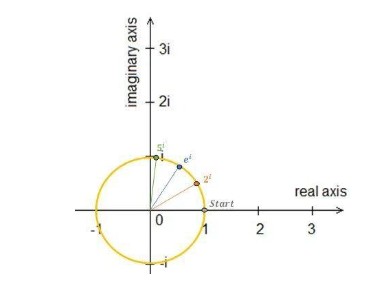
Αν κρατήσουμε σταθερό το αριθμό e στη σχέση 𝒆𝒊𝒙 = 𝐜𝐨𝐬 𝒙 + 𝒊𝒔𝒊𝒏(𝒙) ,για οποιονδήποτε γωνία x, οι συντεταγμένες (cos(x), sin(x)) αντιστοιχούν σε σημείο του τριγωνομετρικού κύκλου.
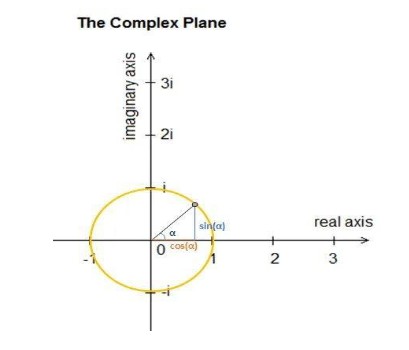
Διαφορετικά, αν κρατήσουμε σταθερό το x, με x=1 και στη θέση του e τοποθετήσουμε οποιονδήποτε αριθμό, τότε το αποτέλεσμα δείχνει την απόσταση που έχει διαγράψει το σημείο στην περιφέρεια του κύκλου από το σημείο (1,0). Για τον αριθμό ε ισχύει ότι αυτή η απόσταση είναι ίση με 1.
Το πρόβλημα των 7 γεφυρών του Köningsberg (The Köningsberg Problem)
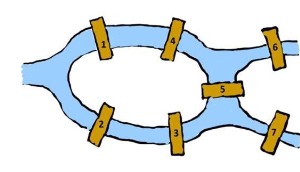 Το Köningsberg, το σημερινό Kaliningrad της Ρωσίας, βρίσκεται δίπλα στον ποταμό Πρέγκελ και έχει δύο νησιά τα οποία επικοινωνούσαν μέσω 7 γεφυρών. Το ποτάμι ρέει γύρω από τα μικρά νησιά, ενώ όλες οι γέφυρες συνδέουν τις όχθες με τα νησιά, εκτός από μία που συνδέει τα δύο νησιά μεταξύ τους.
Το Köningsberg, το σημερινό Kaliningrad της Ρωσίας, βρίσκεται δίπλα στον ποταμό Πρέγκελ και έχει δύο νησιά τα οποία επικοινωνούσαν μέσω 7 γεφυρών. Το ποτάμι ρέει γύρω από τα μικρά νησιά, ενώ όλες οι γέφυρες συνδέουν τις όχθες με τα νησιά, εκτός από μία που συνδέει τα δύο νησιά μεταξύ τους.
Το Köningsberg έγινε ευρύτατα γνωστό μέσω ενός προβλήματος το οποίο θεμελίωσε τη θεωρία γραφημάτων ή αλλιώς τοπολογία. Ο γρίφος είναι ο εξής:
«Κάθε Κυριακή, πολλοί κάτοικοι του Köningsberg συνήθιζαν να κάνουν περιπάτους στις γέφυρες. Είναι δυνατό κάποιος να κάνει τον περίπατό του και να περάσει και από τις 7 γέφυρες, χωρίς να περάσει από κάποια γέφυρα δεύτερη φορά;»
Ο Όιλερ έδωσε την απάντηση στο πρόβλημα όσο βρισκόταν στο πανεπιστήμιο της Αγίας Πετρούπολης. Η απάντηση που έδωσε ήταν ότι δεν υπάρχει τέτοια διαδρομή που να ικανοποιεί το ζητούμενο! Και φυσικά, συνόδεψε την απάντησή του με απόδειξη.
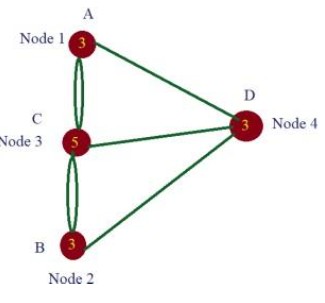
Αναπαριστώντας τα κομμάτια ξηράς με τελείες και τις γέφυρες με γραμμές, δημιούργησε μια απλοποιημένη μορφή του χάρτη της περιοχής.
Ο Όιλερ παρατήρησε ότι για να επιτευχθεί μια τέτοια διαδρομή, κάθε σημείο χρειάζεται να συνδέεται με άρτιο αριθμό γραμμών, έτσι ώστε ο κάθε περιπατητής να εισέρχεται από μία γέφυρα και να εξέρχεται από άλλη.
Στην περίπτωση όμως της έναρξης και λήξης του ταξιδιού, ο περιπατητής αφήνει ένα κομμάτι ξηράς μέσω μίας γέφυρας και αντίστοιχα χρειάζεται μία γέφυρα για να βγει και να ολοκληρώσει το ταξίδι του. Αν το ταξίδι ξεκινά και ολοκληρώνεται σε διαφορετικές τοποθεσίες, τότε οι δύο αυτές εκτάσεις επιτρέπεται να συνδέονται με περιττό αριθμό γεφυρών. Διαφορετικά, αν το ταξίδι ξεκινά και τελειώνει στο ίδιο μέρος, τότε το σημείο αυτό όπως και όλα τα σημεία πρέπει να συνδέονται με άρτιο αριθμό γεφυρών.
Έτσι, ο Όιλερ κατέληξε στο συμπέρασμα ότι μόνο αν ισχύει μία από τις δύο παραπάνω περιπτώσεις, το ταξίδι είναι εφικτό. Στο πρόβλημα όμως του Köningsberg όλες εκτάσεις ξηράς συνδέονται με περιττό αριθμό γεφυρών. Τρία σημεία έχουν 3 γέφυρες και ένα σημείο έχει πέντε.
Το μεγαλείο της απόδειξης του Όιλερ είναι ότι δεν περιορίστηκε στις διαστάσεις της πόλης, αλλά στάθηκε στον τρόπο με τον οποίο συνδέονταν οι γέφυρες με τα νησιά. Με άλλα λόγια, απέδειξε ότι δεν επηρεάζει το πρόβλημα η απόσταση των νησιών ή το μέγεθος των γεφυρών, αλλά ο αριθμός γεφυρών ο οποίος αντιστοιχεί σε κάθε έκταση ξηράς.
Συνεπώς, με αυτή τη λύση στο πρόβλημα του Κöningsberg, ο Όιλερ εισήγαγε έναν νέο όρο στην επιστήμη των μαθηματικών, γνωστό ως θεωρία γραφημάτων ή τοπολογία και έδωσε μια νέα προοπτική στην προσέγγιση προβλημάτων που παρουσιάζονται ως γεωμετρικά.
Οι διαδρομές αυτές που πρότεινε ο Όιλερ πήραν το όνομά του προς τιμήν του.
Ο Γρίφος της Βασιλείας (The Basel Problem)
Το 1644, Ο Pietro Mengoli, Ιταλός μαθηματικός, ασχολήθηκε με ένα πρόβλημα στο οποίο τελικά έδωσε λύση ο Όιλερ. Συγκεκριμένα, προσπάθησε να υπολογίσει το άθροισμα των αντιστρόφων των τετραγώνων των φυσικών αριθμών, δηλαδή:
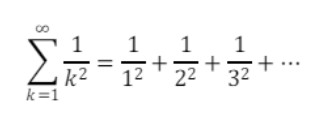
Πριν δώσει ο Όιλερ απάντηση στο παραπάνω πρόβλημα, γνωστοί μαθηματικοί της εποχής όπως ο Jakob Bernouli, ο οποίος χρησιμοποιώντας ανισοτικές σχέσεις κατέληξε σε μία ικανοποιητική προσέγγιση, πως το άθροισμα είναι μικρότερο ή ίσο του 2, αλλά και οι αδερφοί του Johan και Daniel Bernouli που υποστήριξαν ότι είναι περίπου 8/5 και ο Goldbach που ισχυρίστηκε ότι το άθροισμα βρίσκεται μεταξύ του 41/35 και του 5/3. Ο Όιλερ, χρησιμοποιώντας τη σειρά:
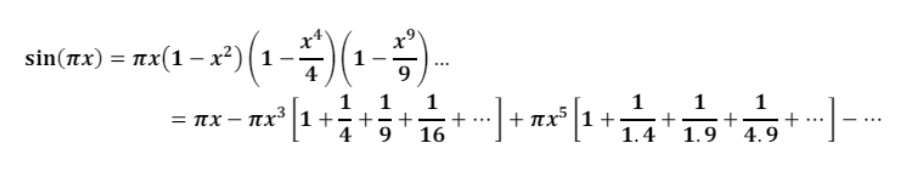
Και γράφοντας τη σειρά Maclaurin για το sin(x):
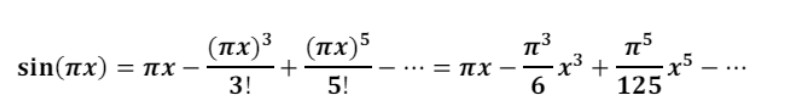
Και συγκρίνοντας τους παράγοντες του x3 από τις δύο σχέσεις κατέληξε στο ότι:
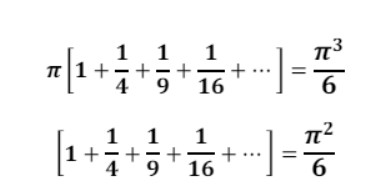
Αν και αυτή η απόδειξη δίχασε τους μαθηματικούς, που μερικοί τη θεώρησαν αρκετά απλή ενώ άλλοι ενδιαφέρουσα, σε κάθε περίπτωση είναι γεγονός ότι για την εποχή που δημοσιεύθηκε ήταν ελλιπής. Χρειάστηκαν 100 χρόνια για να καλυφθούν ορισμένα κενά και να είναι ολοκληρωμένη.
Το συγκεκριμένο πρόβλημα μπορεί να λυθεί και με άλλους τρόπους, όπως με σειρές Fourier, αριθμούς Tamagawa και πολλούς άλλους.
Πάντως, με τη λύση του Όιλερ αποδείχθηκε ότι ο γρίφος της Βασιλείας, που πήρε το όνομά του επειδή οι Bernouli και ο Όιλερ γεννήθηκαν εκεί, συνδέει τη Θεωρία Αριθμών με τη μιγαδική ανάλυση και την αναλυτική γεωμετρία.
Επιλογικά
Με αυτές μόνο τις μικρές αναφορές στο έργο του Όιλερ, διαπιστώνει κανείς την ενασχόληση του μεγάλου μαθηματικού με τους περισσότερους τομείς της μαθηματικής επιστήμης αλλά και την έκταση του συγγραφικού του έργου. Ο Όιλερ αποτέλεσε έμπνευση για τους μετέπειτα μαθηματικούς και δικαίως αναγνωρίστηκε από τους σύγχρονούς του. Πάνω απ’ όλα, όμως, φαίνεται η αγάπη του για το αντικείμενο της επιστήμης του: Το ανήσυχο πνεύμα του που τον παρότρυνε να δώσει εξηγήσεις στα έως τότε ανεξήγητα και οι καινοτόμες λύσεις του είναι ενδεικτικά στοιχεία για το γεγονός ότι προοριζόταν να ασχοληθεί με τις επιστήμες και ειδικά με τα μαθηματικά.
MLA (9th Edition)
- Amber Emmell. “Leonhard Euler and The Basel Problem”. Saint Michael’s College.06/04/2013.https://web.williams.edu/Mathematics/sjmiller/public_html/hudso n/Emmell,%20Amber_Euler%20&%20The%20Basel%20Problem.pdf. Archive
- Brendan W. Sullivan. “The Basel Problem Numerous Proofs”. Carnegie Mellon University.04/11/2013. https://www.math.cmu.edu/~bwsulliv/basel-problem.pdf. Archive
- Carl B. Boyer.“Leonard Euler”. Britannica.02/29/2024.https://www.britannica.com/biography/Leonhard- Euler.Encyclopaedia
- “Euler’s Identity (Complex Numbers)”.YouTube.Uploaded by Mark Newman.2017. https://www.youtube.com/watch?v=sKtloBAuP74.Video
- Harini-jayaraman. “Konigsberg bridge problem and the evolution of Mathematics”.04/29/2022.Lancaster. https://www.lancaster.ac.uk/stor-i-student- sites/harini-jayaraman/konigsberg-bridge-problem-and-the-evolution-of-mathematics/. Website and Internet Images
- “How the Königsberg bridge problem changed mathematics – Dan Van der Vieren”. YouTube.Uploaded by Ted-Ed. 2017.https://www.youtube.com/watch?v=nZwSo4vfw6c. Video
- “Institutiones calculi integralis”. Wikipedia. 05/30/2023. https://en.wikipedia.org/wiki/Institutiones_calculi_integralis.Internet Image
- James Thorn. “Euler’s identity”.Medium.02/19/2020. https://medium.com/swlh/eulers- identity-990b52f0d8fc.Website
- “Leonard Euler”.Wikipedia.03/07/2024.https://en.wikipedia.org/wiki/Leonhard_Euler. Internet Image
- Mike Bertrand. “Reading Euler’s Introductio in Analysin Infinitorum”.Nonagon.11/15/2014. https://nonagon.org/ExLibris/reading-eulers- introductio-analysin-infinitorum. Internet Image
- “The wandering of the imaginary unit”.The unknown X. 01/21/2011. https://thanasiskopadis.blogspot.com/2011/01/h.html. Website
- “Pietro Mengoli”. Wikipedia.1012/2023. https://en.wikipedia.org/wiki/Pietro_Mengoli. Website
- Prabhat Mahato. “The Basel Problem: 1 + 1/2² + 1/3² + …… = π²/6 — Two Simplest Proofs”.Medium. https://medium.com/intuition/two-simplest-proofs-of-the-basel- problem-1-1-2%C2%B2-1-3%C2%B2-%CF%80%C2%B2-6-4b3fe9677334. Website
- Walter Gautschi. “Leonhard Euler: His Life, the Man, and His Works”.Purdue University.2008. https://www.cs.purdue.edu/homes/wxg/EulerLect.pdf. Archive
- Weisstein, Eric W. “Königsberg Bridge Problem.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/KoenigsbergBridgeProblem.html. Website